2024年的AP预备微积分考试已于5月10日星期五举行完毕,不知道大家考的怎么样呢?CB官网也发布了2024年AP预备微积分FRQ真题,今天考而思惟世为大家带来2024年AP预备微积分FRQ考试真题及答案讲解!感兴趣的同学赶紧来看看吧!
整体分析
作为2024年的首考科目,AP预备微积分的北美FRQ题目整体难度不大,FRQ的出题形式和之前官方给出的sample test基本一样,考生如果在考前完整练习过sample test,这套试卷就不会给学生带来过多的挑战。
逐题分析
第一题
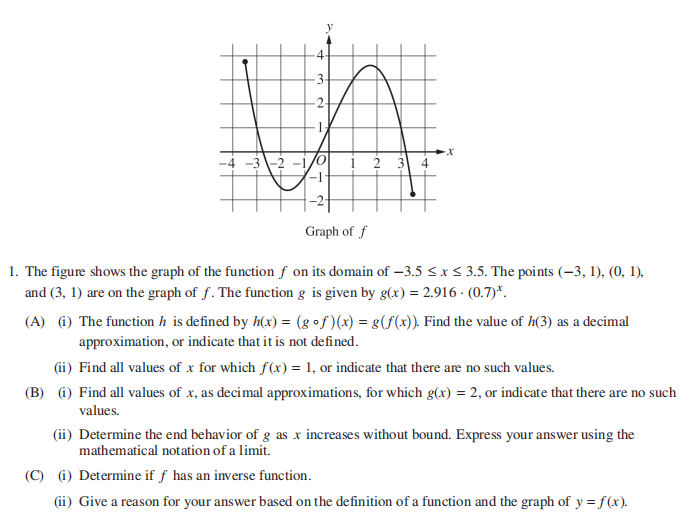
题目给出两个函数,一个以图象形式呈现的多项式函数f(x)和一个有具体表达式的指数函数。
A问解析
1)题目定义了一个新的函数h(x)=g(f(x)), 要求考生找到h(3)的取值,并利用计算器转换成小数。
这一问主要考查复合型函数的计算,我们可以利用f(x)的图象先找到f(3)=1,再把这一数值带入到g(x)的函数表达式,利用计算器求解即可。
2)题目要求考生利用f(x)的图象找到所有满足f(x)=1的取值,我们可以直接在图象中画出一条水平线y=1,观察它和f(x)交点处的x值即可。
B问解析
题目要求考生利用计算器解出man满足g(x)=2的x值,再利用极限的符号描述当x趋近正无穷的时候,函数g(x)的终端趋势(end behavior)。
描述end behavior的时候我们可以直接画出g(x)的图象,观察图象看到趋势。
C问解析
题目要求我们判断f(x)是否有反函数并说明理由,此题为解释说明类题目,答题时需要说明函数f(x)不是一个一对一函数(one-to-one function),所以它没有反函数。
第二题

题目给出了一个卖电子游戏的实际场景,已知时间t=0的时候,卖出游戏数量是40 thousand,时间t=91的时候,卖出游戏数量是76 thousand. 卖出游戏的数量与时间的关系可以用一个对数型函数G(t)=a+bln(t+1)来表示。
A问解析
题目要求考生利用已知信息中给的数据,列出两个能够求解出a和b的方程,并求出a和b的取值。
我们可以把t=0,G=40和t=91,G=76带入到函数表达式中,再借助计算器进行方程组求解,便可得到a和b的取值。
B问解析
1)题目要求考生计算t=0和t=91时,函数的平均变化率(average rate of change)。我们可以直接套用平均变化率的计算公式G(91)-G(0)除以91-0得出结果。
2)题目要求我们利用刚才找到的平均变化率,得到t=50时,卖出游戏数量的近似值。
我们可以把上一问求出的平均变化率作为一条直线的斜率,再利用t=0,G=40或者t=91,G=76,写出这条直线的点斜式方程,之后把t替换成50,得到的y值就是题目想要的答案。
3)题目让我们解释一下为什么当0 此题主要考查图象的凹凸性(concavity),函数作为一个递增的对数型函数,图象呈现出concave down的趋势,此时t=0,G=40和t=91,G=7的两点连线会在0 C问解析 题目告诉我们当t大于91的时候,实际售出的游戏数量在逐渐减少,考生需要解释当t大于91时,为什么我们继续利用函数G(t)计算得到的误差会变大。 G(t)作为对数函数会始终呈现递增的趋势,但实际卖出的游戏数量在逐渐减少,因此会导致函数值和实际值之间的差距越来越大。 第三题 题目给出一个汽车轮子在地面上滚动的例子,半径为9的轮子上有一个点W在t=1/2的时候接触到地面,在t=5/2的时候,W点继续碰到地面。 又已知W点距离地面的最高高度为18,当轮子滚动的时候,W点距离地面的高度呈现出周期性的增加和减小。 题目要求我们利用正弦型函数(sinusoidal function)描述数W点距离地面的高度h与时间t的关系。 A问解析 题目给出一个正弦函数的图象以及5个点,考生需要利用题干信息中的已知条件标出5个点的坐标。 我们可以利用题干信息确定出周期是5/2-1/2=2,h的最大值是18,h的最小值是0,结合图象中5个点的位置便可以确定对应的坐标。 B问解析 题目要求考生找到正弦型函数的具体表达式h(t)=asin(b(t+c))+d。 在具体计算时,我们可以利用5个点的坐标确定出振幅(amplitude)以及竖直方向的平移,从而得到a和d的数值,再利用周期的计算公式可以得到b的取值。 最后选择任意点坐标带入到函数表达式中即可得到c的取值。 C问解析 题目让我们判断图象中某两点间图象的正负性和增减性,以及函数变化率(rate of change)的变化情况。 我们可以直接利用已经标好5点坐标的A问图象,确定函数的正负性和增减性。判断函数变化率的变化情况时可以结合函数的凹凸性(concavity)。 第四题 题目的三个小问相对独立,主要考察不同类型方程的求解以及表达式的化简。 A问解析 题目要求考生分别求解一个包含指数函数的方程和一个包含反三角函数的方程。 在求解指数方程时,可以利用指数和对数间的相互转换把未知数x从次方上面拿下来,从而解出x的值。 求解包含反三角函数的方程时,可以直接转换为三角函数的方程,再利用特殊角的三角函数值解出x值。 B问解析 题目要求考生先对一个对数表达式进行合并,再对一个三角函数表达式进行化简。 合并对数表达式的时候,我们可以利用对数的计算性质讲对数间的加减法进行合并,整理成只有一个对数且对数内部有几项乘除的形式。 化简三角函数表达式的时候,需要利用三角恒等式将1-sin2x和secx分别转化成cos2x和cosx,再利用tanx=sinx/cosx进行改写。 C问解析 题目给出一个反三角函数和三角函数复合后的函数m(x)=cos-1(tan2x),考生需要解出函数值等于0时的x值。 我们可以先利用三角函数去掉反三角函数,再利用特殊角的三角函数值去掉tan,从而解出x值。 以上就是有关2024年AP预备微积分考试FRQ真题及答案讲解,希望对大家有帮助,想要了解更多关于2024年AP考试其他科目真题及答案讲解的,可以多多关注我们哦。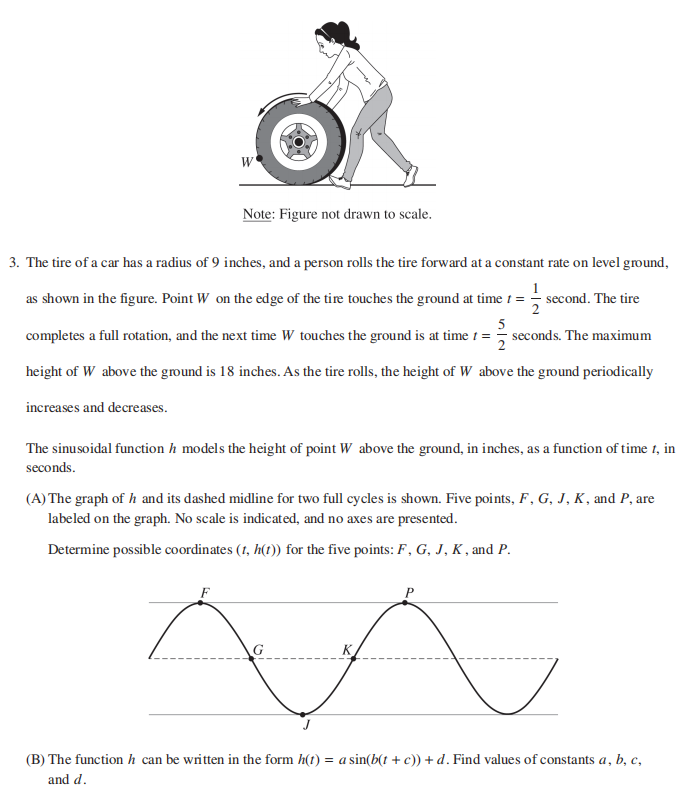


凡来源标注“惟世教育”均为惟世教育原创文章,版权均属惟世教育所有,任何媒体、网站或个人未经本网协议授权不得转载 链接、转贴或以其他任何方式复制、发表。未注明来源等稿件均为转载稿,如涉及版权请联系在线客服处理。
免费获得学习规划方案
已有 2563 位留学生获得学习规划方案



马上领取规划
*已对您的信息加密,保障信息安全。

 在线咨询
在线咨询
 免费通话
免费通话